At any moment when market opens, a
software program that I designed calculates the value of the proprietary
"Investment Value Index" for each of the following five major asset
classes represented by their respective ETFs: cash (SHY), long-term Treasury
bonds (TLT), gold (GLD), stocks (SPY), and real estate (IYR). Then, I allocate
equal capital to the two ETFs with the highest values of the "Investment
Value Index".
For example, suppose on February 1st, 2012, the two assets with the
highest value of the "Investment Value Index" were cash and long-term
Treasury bonds, I would allocate equal amount of capital to SHY and TLT. If on
February 2nd, 2012, the two assets with the highest value of the
"Investment Value Index" changed to gold and long-term Treasury
bonds, I would exchange SHY to GLD, and continue to hold TLT.
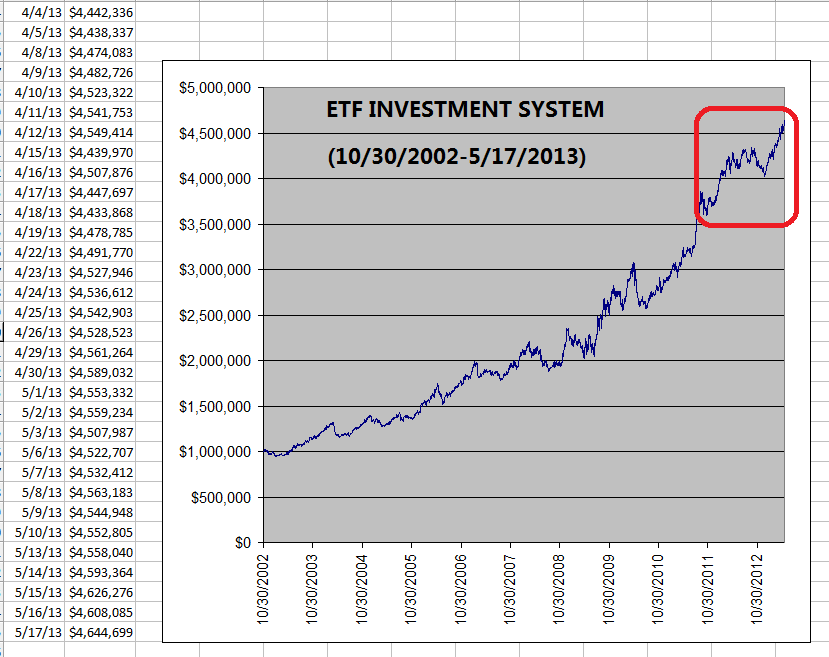
The
following chart is the equity growth curve of the ETF Investment System model
from 10/30/2002 to 9/19/2013:
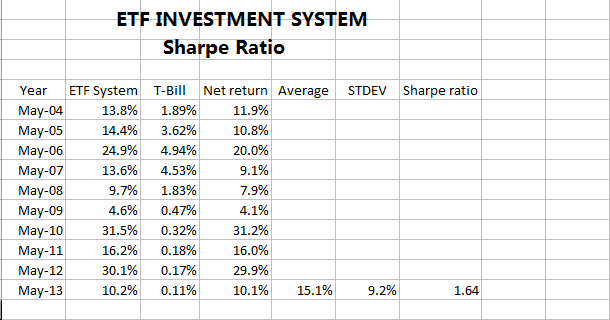
The
following is the Sharpe ratio calculation of the ETF Investment System (Sharpe
ratio 1.4 from January 2004 to September 2013):
Additional
improvement on this very simple yet elegant investment system is as follows.
Suppose
ETF Investment System holds TLT and SPY, each with 50% of total investing
capital. But the volatility of SPY is substantially higher than that of TLT. If
each ETF has the same amount of capital, SPY would contribute more than TLT in
term of both upside and downside. To account for this, volatility adjustment is
needed to balance risk.
Suppose again, ETF Investment System holds SPY
and IYR, each with 50% of total investing capital. But there may be a strong
positive correlation of price movement between SPY and IYR. If each ETF has the
same amount if capital, the SPY and IYR portfolio would have much higher
volatility than the SPY and GLD portfolio, which may have negative correlation
of price movement between the two. In this case, correlation adjustment is
needed to minimize risk.
The
calculation to construct a minimum variance portfolio is shown below.

In this hypothetical
example, SPY and GLD have a negative correlation of –0.6018 and volatility of
GLD is more than double that of SPY. Therefore, allocation of capital should be
70% SPY and 30% GLD to achieve minimum variance.
Indeed, portfolio variance is a very low number
of 0.000014.
Equity
growth curve of the minimum variance ETF Investment System portfolio is shown
below (from 10/30/2002 to 10/11/2013).
Annualized
return: +15.5% (compare to +14.1%
before)
Maximum
drawdown: -13.8% (compare to –15.9% before)
Sharpe ratio: 1.4
(same as before 1.4)
The
following is the Sharpe ratio calculation of the minimum variance ETF
Investment System (Sharpe ratio 1.4 from January 2003 to October 2013).
The
minimum variance ETF Investment System improves the original system
significantly in term of risk reduction. Historical maximum drawdown is reduced
from –15.9% to –13.8%. Average annual return in the past 11 years is also
enhanced from +14.1% to +15.5%. Initial investment
capital is increased to almost 5-fold. Sharpe ratio is maintained at 1.4 as before.
Higher return with much reduced volatility, the
minimum variance ETF Investment System proves to be a worthwhile modification
of the original ETF Investment System.
In some
retirement accounts and pension plans, participants can only invest in 3 of the 5 major
assets: cash, long-term Treasury bonds, and stocks. Therefore, I have modified
the ETF Investment System with these three asset classes.
At any moment
when market opens, a software program that I designed calculates the value of
the proprietary
"Investment
Value Index" for each of the following 3 major asset classes: cash,
long-term Treasury bonds, and stocks. Then I allocate 100% of the capital to
the ETF or mutual fund with the highest value of the "Investment Value
Index".
For example, suppose on February 1st, 2012, the asset with the
highest value of the "Investment Value Index" was cash, I would
allocate 100% of the capital to a money market mutual fund. If on February 2nd,
2012, the asset with the highest value of the "Investment Value
Index" changed to long-term Treasury bonds, I would exchange the money
market mutual fund to a mutual fund holding long-term Treasury bonds.
To
evaluate the long-term effectiveness of the ETF Investment System, I
back-tested with historical data from March 1950 to March 2013 for the
following three asset classes: 3-month Treasury Bills (representing cash),
10-year Treasury bonds (representing long-term bonds), and S&P 500 Index
(representing stocks).
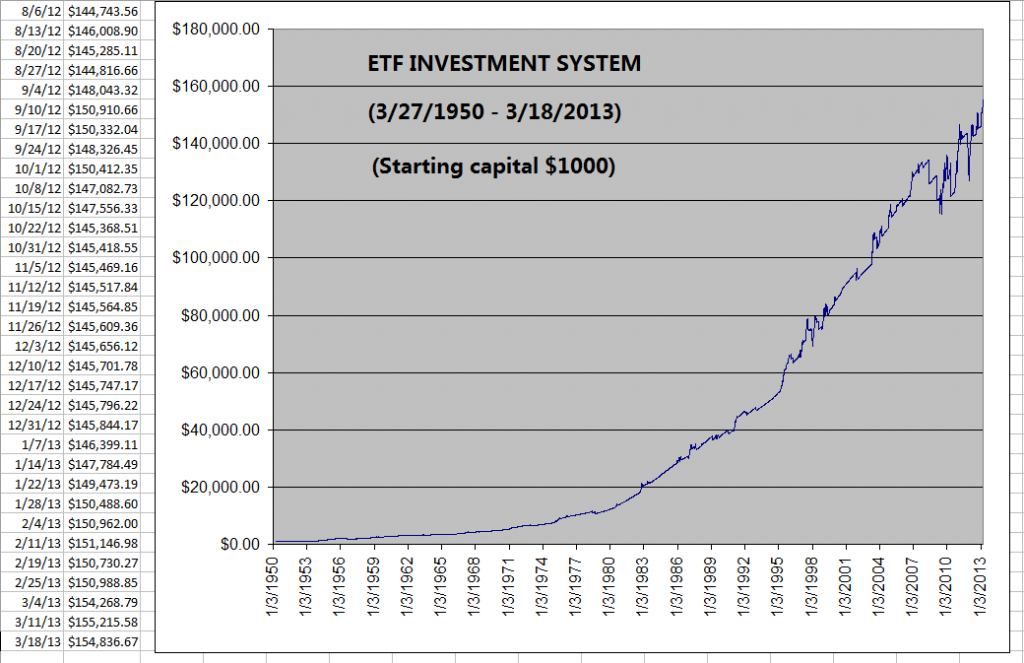
The
following chart is the equity growth curve of the ETF Investment System model
from March 1950 to March 2013 (starting with $1000 initial capital):
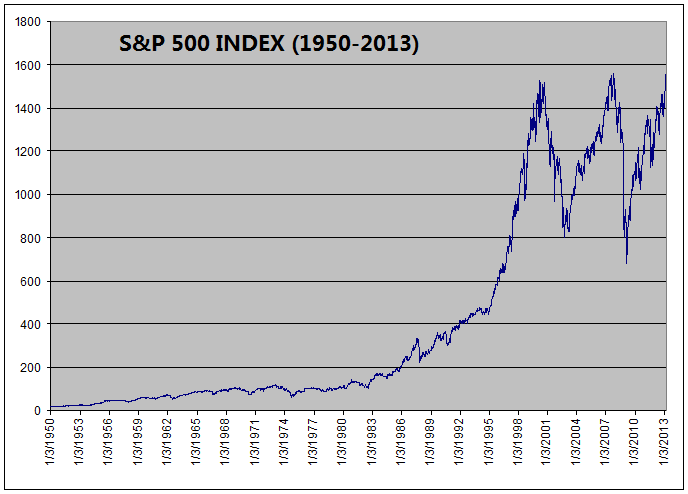
For comparison, this is the
price chart for S&P 500 Index from March 1950 to March 2013:
In
the past 63 years, ETF Investment System increased the initial capital 155
times (from $1,000 to $154,836). Meanwhile, the return for S&P 500 Index
was 90 times (from 17.29 to 1556.89).
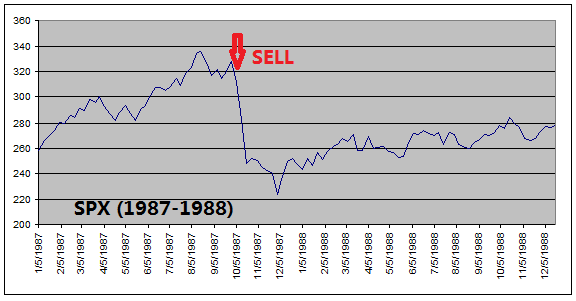
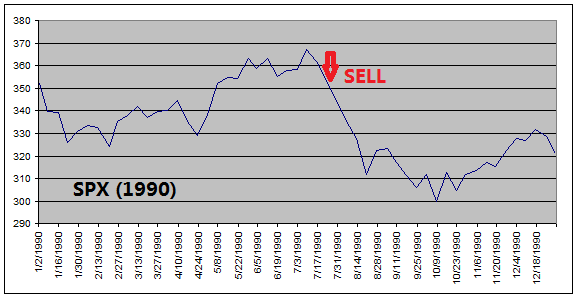
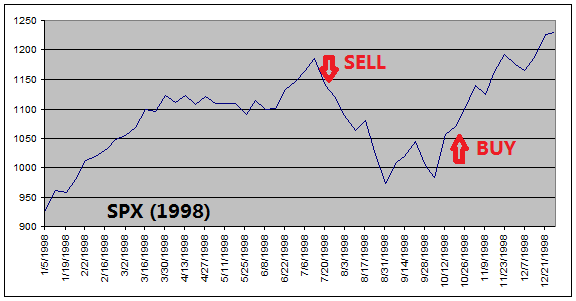
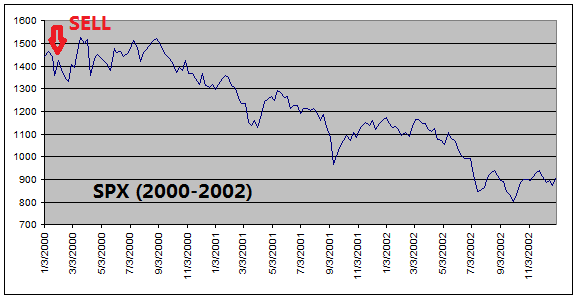
The
reason that ETF Investment System outperforms the equity index is because it
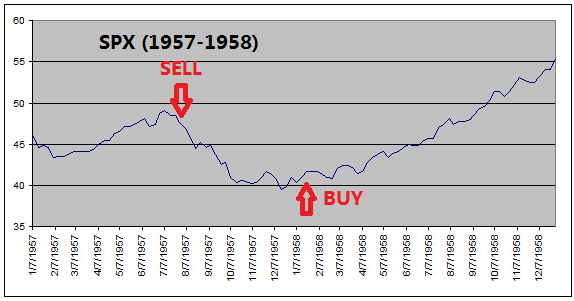
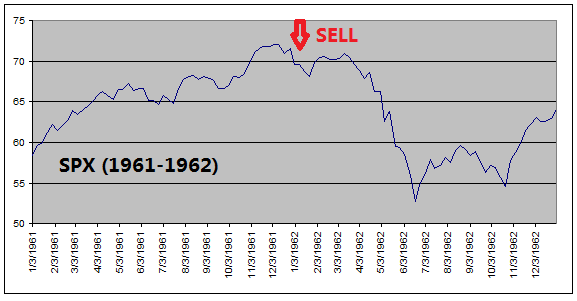
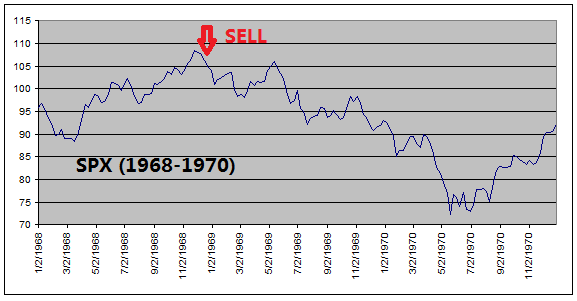
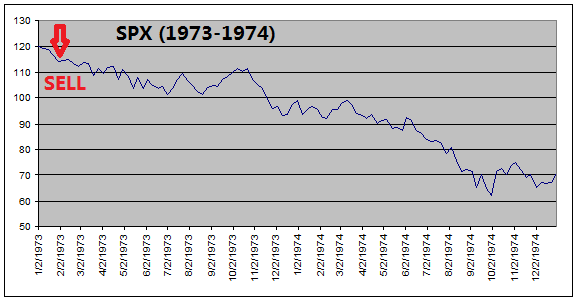
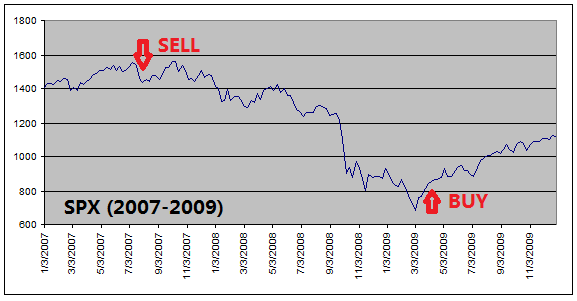
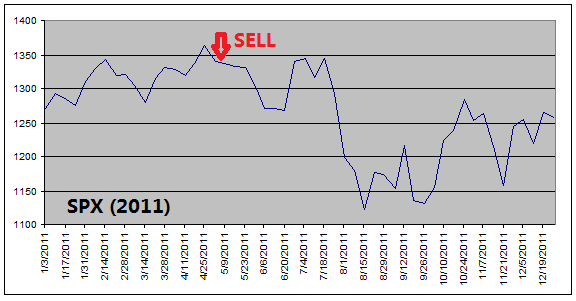
got out of equities before every major stock market downturns (see charts
below).
In summary, ETF Investment System is
a 100% quantitative and mechanical investment system. It holds only 2 of the 5
ETFs of major asset classes at any time (or holds 1 of the 3 ETFs with the ETF
Investment System for retirement accounts). It is simple, easy to follow, and
trades about 25 times per year. Above all, it fulfills the ultimate winning
investment principle of "cut losses short, let profits run".
Disclosure: I hold 2 of the following 5 ETFs in my real brokerage account: SHY,
TLT, GLD, SPY, and IYR.
======
http://murmurhudson.com